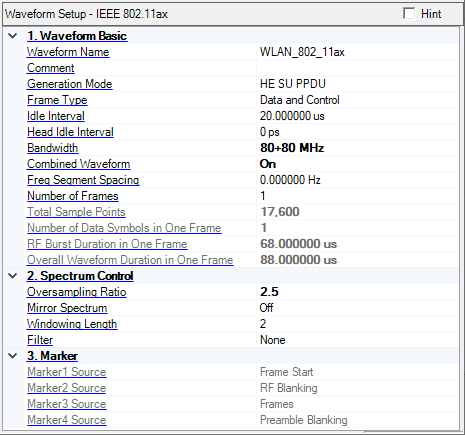
Use this cell to enter a name for the waveform. The alphanumeric text entered in this cell appears in the signal generator's user interface after the configuration is downloaded to the instrument. The signal generator recognizes only waveform names that use the following characters:
A through Z
0 through 9
$ & _ # + - [ ]
If unsupported characters appear in a configuration name, the signal generator generates a "file name not found" error (Error: -256) when you download the configuration to the instrument.
The maximum allowed waveform name length depends on the connected instrument.
For N5182B/N5172B/N5166B/M9383A/M8190A/E6630A/N5106A, it is 150 characters, while for N5182A/E4438C/N8267B, it is 22 characters.
There are cases when multiple waveforms could be downloaded into a single instrument. In this case, to distinguish the waveforms, an index number will be attached at the end of the waveform name. Therefore, the allowed name length will be decremented by 2.
The software initially lets you enter a name with any length characters, but when you click outside of the cell, the software truncates the name to the maximum name length characters.
Enter an alpha-numeric comment of up to 32 characters. The comment resides in the file header and can include spaces and special characters.
Choice: HE SU PPDU | HE Extended Range SU PPDU | HE MU PPDU | HE Trigger Based PPDU | HE NDP | Non-HT
Default: HE SU PPDU
Select the type of frame to be generated.
HE SU PPDU is a standard WLAN 802.11ax Single User PPDU format. It's constructed with legacy preamble, HE preamble and HE data portion and Packet Extension. In contrast, HE NDP format is the same as HE PPDU format without HE data portion. Non-HT refers to the one defined by standard as Non-HT Duplicate Transmission, which is to repeat 802.11a signal in each 20 MHz segment.
Choices: Data and Control | Trigger
Default: Data and Control
This parameter is selectable only when Generation Mode is set to HE SU PPDU, HE MU PPDU, or Non-HT. Otherwise it is read-only and set to Data and Control. When Frame Type is set to Trigger, the trigger frame (a MAC layer frame) structure varies according to the selected Generation Mode, as follows:
For HE SU PPDU, it solicits and allocates resources for UL MU transmissions. An SIFS after the PPDU carries the trigger frame. The trigger frame also carries other information required by the responding STA to send an HE trigger-based PPDU.
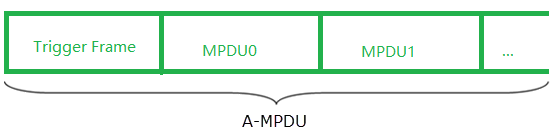
For HE MU PPDU, the transmitted data of each user is always an aggregated MPDU, which contains one trigger frame, and one or more MPDUs, as shown below.
For Non-HT, the PHY should be exactly the same as 802.11a/g if the bandwidth is 20 MHz. When a wider bandwidth is selected, the signal is just a duplication of multiple 20-MHz channels.
For more information on the trigger frame, see the 802.11ax Trigger topic.
Use this cell to set the length (in microseconds) of the idle time after active PPDU frames. This is relevant only in framed mode.
No signal is transmitted during the idle interval, but the MAC layer operates as if a signal is being transmitted.
Set the idle interval ahead of frames in unit of seconds.
Choice: 20 MHz | 40 MHz | 80 MHz | 160 MHz | 80+80 MHz
Default: 20 MHz
Set the number of frames.
Select the bandwidth for IEEE 802.11ax. Please note that the instrument must have at least the equivalent bandwidth to allow the waveform to be successfully transmitted.
The HE extended Range SU PPDU is transmitted only on the primary 20 MHz.
Choice: On | Off
Default: Off
Choose whether to use combined or separate waveforms for the two 80-MHz frequency segments.
Coupled with the number of instruments and the selected Bandwidth.
Range: 0 to 2.4 GHz
Default: 0 Hz
Sets the frequency spacing between two segments of 80+80 for the combined waveform. Its value is limited to an integer multiple of the subcarrier spacing to suppress ICI.
This parameter appears only when Combined Waveform is set to On.
Range: 1 to 2000
Default: 1
Set the number of frames.
This is information indicating the generated waveform length in terms of sampling points.
Number of OFDM Symbols in the Data portion of one frame.
The time duration of RF burst in one frame in unit of seconds.
The time duration of the overall waveform in one frame in unit of seconds.
Range: minimum value is 1
Default: 2
Use this cell to specify the number of times that the baseband signal is oversampled.
A higher oversampling ratio would help simplify the design of transmitting filter, but would result in a longer waveform.
Choice: On | Off
Default: Off
Reverse the spectrum of the waveform. This is useful for systems with external up conversion where the signal spectrum is mirrored by the up conversion process.
On: The Q channel is inverted, resulting in a mirrored spectrum.
Off: The spectrum is not inverted.
Range:
For short guard intervals (400 ns): 0 to 16 samples
For normal guard intervals (800 ns): 0 to 32 samples
Default: 2
Set the duration of the transition time (Ttr) in the windowing function. Ttr creates a small overlap between consecutive subsections in order to smooth the transitions between them. Smoothing the transition is required in order to reduce the spectral sidelobes of the transmitted waveform.
Entering 0 samples means no windowing will be applied. A raised cosine time domain window is applied to the baseband signal to reduce out-of-band power.
A baseband filter is applied to reduce the transmitted bandwidth, increasing spectral efficiency.
For signals generated with digital signal processing, baseband filters are often finite impulse response (FIR) filters with coefficients that represent the sampled impulse response of the desired filter. FIR filters are used to limit the bandwidth of the input to the I and Q modulators.
Five options for baseband filtering can be selected in the Filter Type menu:
None: No filter.
Gaussian: The Gaussian filter does not have zero Inter-Symbol Interference (ISI). Wireless system architects must decide just how much of the ISI can be tolerated in a system and combine that with noise and interference. The Gaussian filter is Gaussian shaped in both the time and frequency domains, and it does not ring like the root cosine filters do. The effects of this filter in the time domain are relatively short and each symbol interacts significantly (or causes ISI) with only the preceding and succeeding symbols. This reduces the tendency for particular sequences of symbols to interact, which makes amplifiers easier to build and more efficient.
Root Raised Cosine: Root raised cosine, also referred to as square root raised cosine, filters have the property that their impulse response rings at the symbol rate. Adjacent symbols do not interfere with each other at the symbol times because the response equals zero at all symbol times except the center (desired) one. Root cosine filters heavily filter the signal without blurring the symbols together at the symbol times. This is important for transmitting information without errors caused by ISI. Note that ISI does not exist at all times, only at the symbol (decision) times.
You can change the values of the Root Raised Cosine Filter to optimize for better spectral characteristics (sharper roll-off on the band edges resulting in less adjacent channel power) vs. better EVM.
However, to reduce the value of Alpha will make the roll-off sharper but cause worse EVM.
Ideal Lowpass: In the frequency domain, this filter appears as a low-pass, rectangular filter with very steep cut-off characteristics. The pass band is set to equal the symbol rate of the signal. Due to a finite number of coefficients, the filter has a predefined length and is not truly "ideal." The resulting ripple in the cut-off band is effectively minimized with a Hamming window. This filter is recommended for achieving optimal ACP. A symbol length of 32 or greater is recommended for this filter.
User Defined: Allows you to select a simple unformatted text file (*.txt) of coefficient values, characterizing a user-defined filter. Each line in the file contains one coefficient value. The number of coefficients listed must be a multiple of the selected oversampling ratio. Each coefficient applies to both I and Q components.
The symbol length of the filter determines how many symbol periods will be used in the calculation of the symbol. The filter selection influences the symbol length value.
The Gaussian filter has a rapidly decaying impulse response. A symbol length of 6 is recommended. Greater lengths have negligible effects on the accuracy of the signal.
The root cosine filter has a slowly decaying impulse response. It is recommended that a long symbol length, around 32, be used. Beyond this, the ringing has negligible effects on the accuracy of the signal.
The ideal low pass filter also has a very slow decaying impulse response. It is recommended that a long symbol length, 32 or greater, be used.
For both root cosine and ideal low pass filters, the greater the symbol length, the greater the accuracy of the signal. Try changing the symbol length, and plotting the spectrum to view the effect the symbol length of the filter has on the spectrum.
This cell sets the filter's bandwidth-time product (BT) coefficient. It is valid only for a Gaussian filter.
B is the 3 dB bandwidth of the filter and T is the duration of the symbol period. BT determines the extent of the filtering of the signal. Occupied bandwidth cannot be stated in terms of BT because a Gaussian filter's frequency response does not go to zero, as does a root cosine filter. Common values for BT are 0.3 to 0.5. As the BT product is decreased, the ISI increases.
This cell sets the filter's alpha coefficient. It is valid only for root cosine filters.
The sharpness of a root cosine filter is described by the filter coefficient, which is called alpha. Alpha gives a direct measure of the occupied bandwidth of the system and is calculated as: occupied bandwidth = symbol rate X (1 + alpha). If the filter had a perfect (brick wall) characteristic with sharp transitions and an alpha of zero, the occupied bandwidth would be: symbol rate X (1 + 0) = symbol rate. An alpha of zero is impossible to implement. Alpha is sometimes called the "excess bandwidth factor" as it indicates the amount of occupied bandwidth that will be required in excess of the ideal occupied bandwidth (which would be the same as the symbol rate).
At the other extreme, take a broader filter with an alpha of one, which is easier to implement. The occupied bandwidth for alpha = 1 will be: occupied bandwidth = symbol rate X (1 + 1) = 2 X symbol rate. An alpha of one uses twice as much bandwidth as an alpha of zero. In practice, it is possible to implement an alpha below 0.2 and make good, compact, practical radios. Typical values range from 0.35 to 0.5, though some video systems use an alpha as low as 0.11.
This cell sets the effctive bandwidth for the ideal low pass filter. It is valid only for low pass filters.
This is valid only for user-defined filters.
When you select User Defined
as the filter type, click the 
button in this cell to select a simple unformatted
text file (*.txt) of coefficient values, characterizing a user-defined
filter. Each line in the file contains one coefficient value. The number
of coefficients listed must be a multiple of the selected oversampling
ratio. Each coefficient applies to both I and Q components.
Frame Start - It indicates the beginning of each frame. It starts at the beginning of the Head Idle Interval.
RF Blanking - It controls On/Off of the RF signal. There is a 500 ns pre-blanking before the Preamble part and a 335 ns latency after the Data part for Marker2.
Frames - It indicates the period of each frame. The Head Idle Interval is included in the frame, and the Idle Interval is excluded.
Preamble Blanking - It indicates the Preamble part of each frame.